Velocidad (MRU y MRUA) - ACADEMIA AYUDA ACTIVA

Ejercicio 1: Gráfico espacio-tiempo.

a) Calcule la velocidad en cada tramo.

b) Indicar si la aceleración es positiva o negativa en cada tramo.

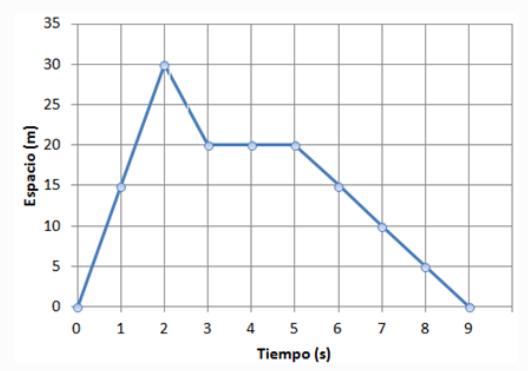
Solución ejercicio 1

Tramo 1 (desde s=0 hasta s=2) -> Velocidad = 15 m/s -> aceleración>0
Tramo 2 (desde s=2 hasta s=3) -> Velocidad = -10 m/s -> aceleración<0
Tramo 3 (desde s=3 hasta s=5) -> Velocidad = 0 m/s -> aceleración=0
Tramo 4 (desde s=5 hasta s=9) -> Velocidad = -5 m/s -> aceleración<0

Ejercicio 2: Gráfica espacio-tiempo.

a) Calcule la velocidad en cada tramo.

b) Indicar si la aceleración es positiva o negativa en cada tramo

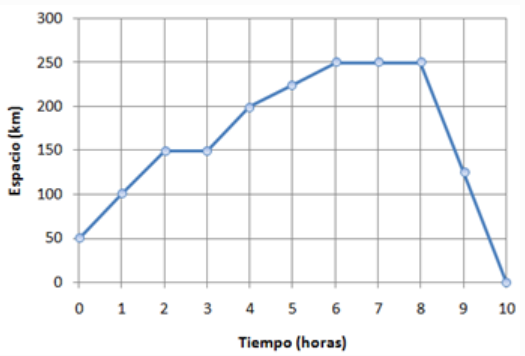
Solución ejercicio 2:

Tramo 1 (desde h=0 hasta h=3) -> Velocidad = 50 km/h -> aceleración>0
Tramo 2 (desde h=2 hasta h=3) -> Velocidad = 0 km/h -> aceleración=0
Tramo 3 (desde h=3 hasta h=4) -> Velocidad = 50 km/h -> aceleración>0
Tramo 4 (desde h=4 hasta h=6) -> Velocidad = 25 km/h -> aceleración>0
Tramo 5 (desde h=6 hasta h=8) -> Velocidad = 0 km/h -> aceleración = 0
Tramo 6 (desde h=8 hasta h=10) -> Velocidad = -125 km/h -> aceleración<0

Ejercicio 3: Gráfico velocidad-tiempo.

a) Identifica el tipo de movimiento (MRU o MRUA) en cada tramo.

b) Calcula la aceleración en cada tramo.

c) Calcular el espacio recorrido en cada tramo.

d) Calcular el espacio total recorrido.

e) Calcular la velocidad media.

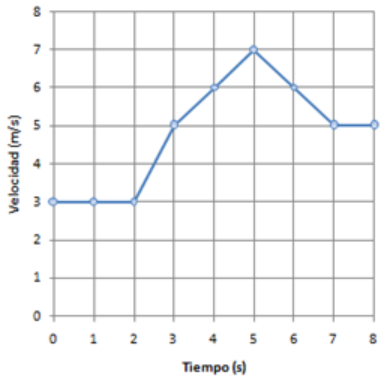
Solución ejercicio 3:

Tramo 1 (desde s=0 hasta s=2) -> MRU -> Aceleración = 0 m/s² -> Espacio recorrido: s1 = s0 + v x t = 6m
Tramo 2 (desde s=2 hasta s=3) -> MRUA -> Aceleración = 2 m/s² -> Espacio recorrido: s1 = s0 + v0 x t + 1/2 x a x t² = 0 + 3 x 1+1/2 x 2 x 1² = 4m
Tramo 3 (desde s=3 hasta s=5) -> MRUA -> Aceleración = 1 m/s² -> Espacio recorrido: s1 = s0 + v0 x t + 1/2 x a x t² = 0 + 5 x 2+1/2 x 1 x 2² = 12m
Tramo 4 (desde s=5 hasta s=7) -> MRUA -> Aceleración = -1 m/s² -> Espacio recorrido: s1 = s0 + v0 x t + 1/2 x a x t² = 0 + 7 x 2+1/2 x (-1) x 2²=12m
Tramo 5 (desde s=7 hasta s=8) -> MRU -> Aceleración = 0 m/s² -> Espacio recorrido: s1 = s0 + v * t = 0 + 5 x1 = 5m

Espacio total recorrido = 6+4+12+12+5 = 39 metros

Velocidad media = espacio total recorrido / tiempo total empleado = 39 / 8 = 4,875 m/s

Ejercicio 4: Gráfico velocidad-tiempo

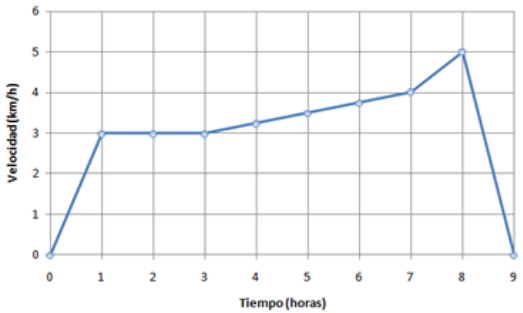
a) Identifica el tipo de movimiento (MRU o MRUA) en cada tramo.

b) Calcula la aceleración en cada tramo.

c) Calcular el espacio recorrido en cada tramo.

d) Calcular el espacio total recorrido.

e) Calcular la velocidad media.

Solución ejercicio 4:

Tramo 1 (desde h=0 hasta h=1) -> MRUA -> Aceleración = 3 km/h² -> Espacio recorrido: 1,5km
Tramo 2 (desde h=1 hasta h=3) -> MRU -> Aceleración = 0 km/h² -> Espacio recorrido: 6km
Tramo 3 (desde h=3 hasta h=7) -> MRUA -> Aceleración = 0,25 km/h² -> Espacio recorrido: 14km
Tramo 4 (desde h=7 hasta h=8) -> MRUA -> Aceleración = 1 km/h² -> Espacio recorrido: 4,5km
Tramo 5 (desde h=8 hasta h=9) -> MRUA -> Aceleración = -5 km/h² -> Espacio recorrido: 7,5km

Espacio total recorrido = 1,5+6+14+4,5+7,5 = 33,5 metros

Velocidad media = espacio total recorrido / tiempo total empleado = 33,5 / 9 = 3,72 km/h

Ejercicio 5: Resuelve los siguientes casos de MRU

¿A qué velocidad debe circular un auto de carreras para recorrer 50 km en un cuarto de hora?
Una bicicleta circula en línea recta a una velocidad de 15 km/h durante 45 minutos. ¿Qué distancia recorre?
Calcula la distancia que recorre en 20 min una moto que se desplaza a 90 Km/h
Calcula la distancia que recorre un caracol en 5 min si se desplaza en línea recta 10,8 m en 1,5 h.
Calcula el tiempo que invierte una avioneta en un viaje de 1656 Km si su rapidez media es de 720 Km/h

Solución ejercicio 5

Xf = X₀ + v ∙ (tf-t0) → 50 = 0 + v ∙ 1/4 → t = 200 km/h
Xf = X₀ + v ∙ t→ xf = 0 + 15 ∙ 45/60 → t = 11,25 km/h
Xf = X₀ + v ∙ (tf-t0) = 0 + 90 ∙ (20/60 – 0) = 30k
Xf = X₀ + v ∙ (tf-t0) = 0 + v ∙ (5/60 – 0) → calcular v = 10,8/1,5 = 7,2 m/h → Xf = 0 + 7,2 ∙ (5/60 – 0) = 0,6 m
Xf = X₀ + v ∙ (tf-t0) → 1656=0+ 720 ∙ t → t = 2,3h = 2 h y 18 min

Ejercicio 6: Resuelve los siguientes casos de MRUV

Un automovil pasa de 6 m/s a 10m/s en un tiempo de 5 segundos. Calcula aceleración.
Un motorista circula a 4m/s y acelera durante 2s a 1,5m/s². Calcula su velocidad al cabo de estos dos segundos.
Un cohete parado, se aleja de la Tierra con aceleración de 5m/s². Calcula qué altura habrá ascendido en 10 segundos.
Un cuerpo posee una velocidad inicial de 12 m/s y una aceleración de 2 m/s² ¿Cuánto tiempo tardará en adquirir una velocidad de 144 Km/h?
Un móvil lleva una velocidad = 8 cm/s y recorre una trayectoria rectilínea con aceleración igual a 2 cm/s². Calcular el tiempo que ha tardado en recorrer 2.10 m.

Solución ejercicio 6

a= (vf-v0)/t = (10-6) / 5 = 0,8 m/s²
vf = v0 + a ∙ t = 4 + 1,5 x 2 = 7 m/s
xf= x0 + v0 ∙ t + 1/2 ∙ a ∙ t² = 0 ∙ 10 +1/2 ∙ 5 ∙ 10² = 250 m
a= (vf-v0)/t -> 2 = (40-12) / t -> t = 14s
xf= x0 + v0 ∙ t + 1/2 ∙ a ∙ t² -> 210 = 0,08 ∙ t +1/2 ∙ 0,02 ∙ t² -> t=11,03s

Ejercicio 7: encuentro en MRU:

Un coche sale a 110 km/h en un sentido y en otro sentido sale una moto a 70km/h. Si la distancia entre ellos es de 360km.

a) ¿Cuánto tiempo tardan en encontrarse?

b) ¿En qué km se encuentran?

Solución ejercicio 7:

a) Construir un sistema teniendo en cuenta la distancia total.

Aplicamos fórmula velocidad al coche: V = e/t → 110 = (360-e)/t (Introducir distancia total)

Aplicamos fórmula velocidad a la moto: V = e/t → 70 = e/t → e = 70t

Resolvemos el sistema despejando t: 110 = (360-70t)/t→ t = 2h

b) Resolvemos el sistema despejando e

V= e/t → 110 = e/2 → e = 220km

Ejercicio 8: alcance en MRU:

Un coche sale a las 9.00 a 60km/h y a las 11.00 sale una moto a 100km/h.

a) ¿Cuánto tiempo tardan en encontrarse?

b) ¿En qué km se encuentran?

Solución ejercicio 8:

a) Construir un sistema teniendo en cuenta la diferencia de horario.

Aplicamos fórmula velocidad al coche: v = e/t → 60=e/t

Aplicamos fórmula velocidad a la moto: v=e/t → 110 = e /(t-2) (Introducir la diferencia de tiempo)

Resolvemos el sistema despejando t: 60t = 110 (t-2) → t=5h

b) Resolvemos el sistema despejando e:

60 = e/5 → e= 300km