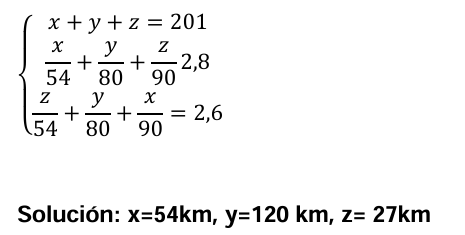EJERCICIOS SISTEMA DE ECUACIONES
1. EJERCICIO: Cierta marca de pintura es elaborada con tres ingredientes A, B y C, comercializándose en tres tonos diferentes. El primero se prepara con 2 unidades de A, 2 de B y 1 de C; el segundo con 1 unidad de A, 2 de B y 2 de C; y el tercero con una unidad de cada ingrediente. El bote del primer tono se vende a 23 euros, el segundo a 17 euros y el tercero a 14 euros. Sabiendo que el margen comercial (o ganancial) es de 3 euros por bote, ¿qué precio por unidad le cuesta a dicha marca de pintura cada uno de los tres ingredientes?
Solución
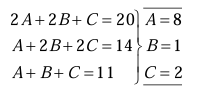
2. EJERCICIO: Una fábrica de chocolates emplea, para una determinada marca, leche, cacao y almendras, siendo la proporción de leche el doble que la de cacao y almendras juntas. Los precios de los ingredientes por kilo son: leche, 0,80 euros; cacao, 4 euros; y almendra, 10 euros. En un día se fabrican 9 000 kg de chocolate de dicha marca con un coste total de 22 800 euros. ¿Cuántos kg se utilizan de cada componente al día?
Solución
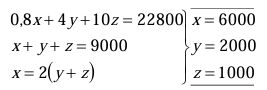
3. EJERCICIO: Para un determinado partido de fútbol se ponen a la venta tres tipos de localidades: fondo, general y tribuna. Se sabe que la relación entre los precios de las localidades de tribuna y general es de 19/18 y entre general y fondo es de 6/5. Si al comprar tres localidades, una de cada caso, se pagan en total 52 euros, ¿cuál es el precio de cada tipo de localidad?
Solución
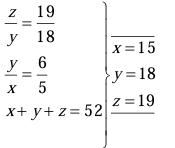
4. EJERCICIO: Un tren transporta 500 viajeros y la recaudación de sus billetes asciende a 2 142 euros. Calcular cuántos viajeros han pagado el importe total del billete, que vale 9 euros; cuántos han pagado el 20% del billete y cuántos el 50%, sabiendo que el número de viajeros que han pagado el 20% del billete es el doble del número de viajeros que pagan el billete entero.
Solución
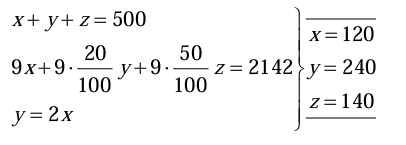
5. EJERCICIO: Andrés, Juan y Luis son tres amigos. Hablando un buen día sobre sus edades observan que: “El doble de la edad de Andrés más el triple de la edad de Juan es tres años superior a cuatro veces la edad de Luis. El triple de la edad de Luis menos el doble de la edad de Juan es siete años inferior al doble de la edad de Andrés. El doble de las edades de Andrés y Luis es tres años inferior a cinco veces la edad de Juan”. ¿Cuál es la edad de cada uno de los amigos?
Solución
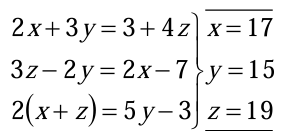
6. EJERCICIO: Un país importa 21 000 vehículos mensuales de 3 marcas A, B, C, al precio de 7500; 9100 y 12000 euros, respectivamente. Si el total de la importación asciende a 201,8 millones de euros y de la marca A importa el 40% de las otras dos marcas juntas, ¿cuántos vehículos de cada mar entran en el país?
Solución
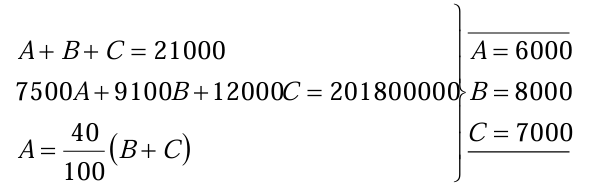
7. EJERCICIO: Una tienda ha vendido 600 ejemplares de un videojuego por un total de 6384€. El original costaba 12€, pero también ha vendido copias, presuntamente defectuosas, con un descuento del 30% y 40%. Sabiendo que el número de copias vendidas fue la mitad del de originales, calcular a cuántas copias se le aplicó el descuento del 30%.
Solución

8. EJERCICIO: Hallar un número de 3 cifras, sabiendo que suman 9, que si al número dado se le resta el que resulta de invertir el orden de sus cifras, la diferencia es de 198; y que además, la cifra de las decenas es la media aritmética de las otras dos.
Solución
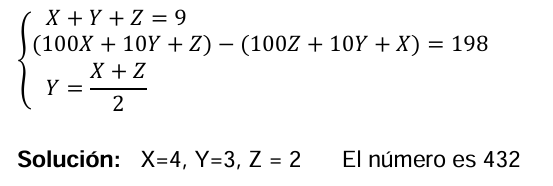
9. EJERCICIO: Averigua la edad de tres hermanos, sabiendo que el triple de la edad del primero menos el doble de la edad del segundo más la del tercero hacen un total de 22 años; la edad del primero menos la del segundo más el doble de la del tercero son 8 años; y el doble de la del primero más la del segundo menos la del tercero son 20 años.
Solución

10. EJERCICIO: La distancia de tres playas (A, B, C) al lugar de veraneo de una familia es tal que el doble de la distancia de A es el triple de la distancia a B. La suma de las distancias A, B y C es de 90.000m, y el doble de la distancia a B más el triple de la distancia a C menos la distancia a A es igual a 130.000 m. ¿Cuál es la distancia de cada playa?
Solución

11. EJERCICIO: Una papelería tiene un total de 270 bolígrafos de tres tipos x, y, z . Del tipo x tienen 30 unidades menos que de la totalidad de y más z, y del tipo z tienen el 35% de la suma de x más y. ¿Cuántos bolígrafos de cada tipo hay en la librería?
Solución
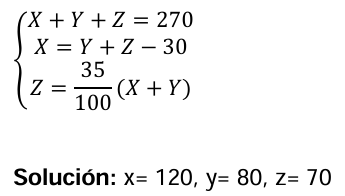
12. EJERCICIO: 2) Un vehículo todo terreno sube las cuestas a 54 km/h, las baja a 90 km/h, y en llano lleva una velocidad de 80 km/h. Para ir de una ciudad a otra que dista de ella 201 km emplea 2,8 horas y para volver 2,6 horas. ¿Cuántos kilómetros de camino llano hay entre ambas ciudades?
Solución