INTERÉS SIMPLE
>Un inversor deposita 10.000 € en una cuenta de ahorro durante 3 años. El banco le aplica diferentes tipos de interés simple cada año:
Año 1: 3% anual – Año 2: 4% anual – Año 3: 5% anual
a) Determinar el capital final.
b) Calcular el interés generado cada año.
c) Calcular el interés total acumulado al final de los 3 años.
Solución: a) 11.200€ b) 300, 400 y 500 c) 1.200€
>¿Si voy a invertir mi dinero que opción me interesa más?
a) 15% anual
b) 8% semestral
c) 1% mensual
d) 5% trimestral
Solución: Opción b.
>En el banco A un pagaré de 500€ tiene un tanto de descuento simple del 8% anual. En el banco B el mismo pagaré tiene un tanto de interés simple del 7% anual. Plazo vencimiento: 1 mes.
a) ¿Qué opción resulta más conveniente para descontar el nominal al momento actual? Calcular los capitales en t=0 para comparar.
b) ¿Cúal sería el tanto de interés equivalente del banco A?
Solución: a) Preferible opción B. b) i = 8,7%
>Un cliente nos entrega un efecto comercial de nominal 4.500 € y vencimiento 3 meses, y decidimos descontarlo en una entidad financiera, que nos ofrece cuatro posibilidades:
a) Descuento comercial al 8% anual.
b) Descuento al 8% anual por vencido.
c) Descuento al 7,6% anual por anticipado.
d) Descuento racional al 8,2% anual.
¿Qué opción elegiría usted, y qué importe recibiría con esa opción?
Solución: Opción c) 4.414,5€
>Para que nos descuenten un efecto de nominal 67.000 €. Y con vencimiento dentro de tres meses tenemos dos posibilidades:
– Descuento comercial al 6,75%
– Descuento racional al 6,75 %.
¿Cuál resulta más conveniente y cuánto cobraremos en ella?
Solución: Racional, 65.888,14€
>Se quiere sustituir dos capitales de 800€ que vencen en el mes 5 y mes 8 por un sólo capital en mes 10. Calcular si el tipo de interes anual simple para el primer semestre es del 2% y para el resto 3%.
Solución: 1613,33€
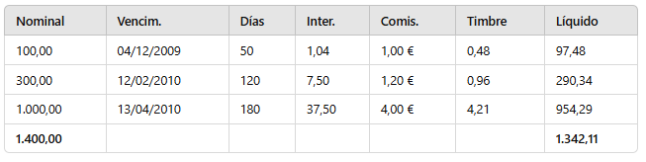
>Hoy 15/10/x una empresa manda a descontar tres efectos. Un efecto A de 100€ que vence el 4/12/x, un efecto B de 300€ que vence el 12/2/x y un efecto C de 1.000€ que vence el 13/4/x. El banco aplica un 7,5% de tasa de descuento (intereses), un 0,4% de comisión (mínimo 1€) y un timbre de 0,48 para el efecto A, 0,96 para el efecto B y 4,21 para el efecto C. Calcular rentabilidad efectiva, rentabilidad tae y i rentabilidad del banco del primer efecto.
Solución:
i efectiva= 20,4% i tae= 7,9% i banco= 16,2%
INTERÉS COMPUESTO
>¿Si voy a invertir mi dinero que opción me interesa más?
a) 15% anual
b) 8% semestral
c) 1% mensual
d) 5% trimestral
Solución: Opción d.
>Un capital se invierte durante 12 meses al 5% de interés efectivo anual. Sabiendo que los intereses del último mes fueron de 35€, calcular el importe invertido.
Solución: 8215,42€
>Los tantos de interés que ofrecen distintas entidades para depósitos a un año son los siguientes:
a) 6,12% anual efectivo.
b) 6% nominal anual capitalizable trimestralmente.
c) 3% semestral efectivo.
¿Cuál es la opción más favorable para nosotros si nos planteamos realizar un depósito?.
¿Qué cantidad podremos retirar dentro de 3 años si depositamos 1.000 euros hoy, y nos aplican el 6% nominal anual capitalizable trimestralmente durante el primer año, y el 3% semestral efectivo durante los 2 años restantes?
Solución: Opción b) 1.194,57€
>Un capital de 100.000 € se ha colocado en una entidad financiera que computa intereses anualmente. Transcurridos n años se forma un montante de 150.583,31 €. Los intereses que se han generado durante el último año ascienden a 7.511,28 €. Calcula:
(a) Tipo de interés efectivo anual al que ha estado colocado este capital.
(b) El tanto nominal capitalizable trimestralmente y el tanto instantáneo equivalentes al tipo de interés obtenido en el apartado anterior.
(c) El número de años que ha durado la operación.
Solución: a) 5,25% b) 5,15% y 5,117% c) 8 años
>Al contratar un depósito, de nominal 18.000€ y por tres años y medio, distintas entidades financieras nos ofrecen las siguientes rentabilidades:
Entidad A : 4% nominal con capitalización mensual.
Entidad B : 4% nominal con capitalización semestral.
Entidad C : 4% nominal con capitalización continua.
(a) ¿Cuál es nuestra mejor opción, y qué cantidad podremos retirar al final de la operación?
(b) Una entidad financiera aplica un 5% por anticipado en sus operaciones de descuento a 4 meses. ¿Qué tanto de interés por vencido debería de cobrar en estas operaciones para seguir obteniendo los mismos beneficios?
Solución: a) Entidad C 20.704,93€ b) 5,0847%
>Un señor obtiene un préstamo de 112.000 € para amortizar por el sistema francés en 10 años y al 8% anual compuesto. En el momento de satisfacer la quinta anualidad acuerda con el prestamista en entregar solamente 5.000 €. A partir del siguiente año y hasta el último entregará la anualidad necesaria para amortizar la deuda. ¿Cuál será la deuda a finales del 5ª año una vez entregados los 5.000 €?
Solución: 78.334,83€
TEORÍA
CAPITALIZACIÓN Y DESCUENTO:
– En una operación financiera, cuanto mayor sea su duración, mayores serán los intereses a acumular o a descontar (según la operación se valore con una ley de capitalización o de descuento).
– A mayor duración mayor será el valor capitalizado. Si fuera descontar menor sería el valor descontado.
– K= periodo de liquidación o frecuencia de cálculo del interés, devengo o fraccionamiento
– Conforme mayor sea la frecuencia de capitalización más crecerán los intereses en interés compuesto en una operacion financiera.
– Factor de capitalización es (1+i·n) en interés simple ó (1+i)n en interés compuesto
– Factor de descuento es (1-dn) en interés simple ó (1-d)n en interés compuesto
– La tasa de descuento o tanto anticipado (d) se aplica a Cn y lo que genere se cobra/paga al inicio de la operación
– La tasa de interés o tanto vencido (i) se aplica sobre C0 y lo que genere se cobra/paga al final de la operación.
-Si tasa de interés es igual a la tasa de descuento (i=d) entonces Dc>Dr.
– Si descuento comercial es igual al descuento racional (Dc=Dr) entonces i>d
– Tipo nominal= tipo contractual: es el tipo de interés pactado entre las partes y plasmado en el contrato. No incluye ninguna característica comercial.
– Tipo efectivo = tipo real: es una medida del coste/ganancia real de una operación teniendo en cuenta las cantidades realmente pagadas/cobradas. Es un dato que se obtiene a posteriori una vez cerrada la operación. Incluye todas las características comerciales (financieras o fiscales). Es un valor anual calculado con leyes compuestas. Refleja el coste o rentabilidad total de la operación.
– Tae: es el tipo de interés que incluye sólo algunas características comerciales. Es calculado teniendo en cuenta los importes que afectan a la entidad-cliente no cliente-terceros.
– Relación coste efectivo y tae:
Coste efectivo > tae (si hay comisiones o impuestos)
Coste efectivo = tae (si no hay comisiones ni impuestos)
– Relación entre i y j según la frecuencia de capitalización k-ésimos del periodo:
Si k>1(mensual, trimestral, semestral,…) entonces i > j
Si k=1 (anual) entonces i = j
Si k<1 (bienal, trienal, …) entonces i < j
– Los intereses que se acumulen o descuenten son siempre proporcionales a la cuantía
– Los intereses generados en IS son proporcionales al capital inicial I= C0 x n x i
– Si t=1 año el capital final a interés simple es igual al capital final a interés compuesto.
– Siempre se cumple 1+i = e j∞
– En capitalización simple el capital crece de forma constante en progresión aritmética. Convenio lineal. Razon I.
– En capitalización compuesta el capital crece de forma variable en progresión geométrica. Convenio exponencial. Razón (1+i).
– En el sistema de capitalización compuesta, los intereses producidos en cada periodo varían en progresión geométrica de razón 1+i.
– Vencimiento común: es la fecha única a la que se trasladan varios capitales con vencimientos distintos, para poder sustituirlos por un solo capital equivalente.
– Capital común: es el capital equivalente al que se transforman varios capitales distintos cuando se quiere compararlos o agruparlos en una misma fecha.
– Vencimiento medio: es la media ponderada de los vencimientos de diferentes capitales
– Reserva matemática o saldo financiero en t: es el capital que mide la diferencia entre los compromisos ya cumplidos en t y los que faltan por cumplir
– La liquidación de cuentas se realiza por el método hamburgués
– En una operación a plazo el comprador es alcista (espera que el mercado suba para la fecha de liquidación) y el vendedor es bajista (espera que el mercado baje para la fecha de liquidación). Es decir quien compra espera revalorización y el que vende caída de precios.
– Letras tesoro se emiten a un precio inferior al valor nominal. Se denomina emisión al descuento.
– El banco de España obliga a informar de las operaciones en tipo de interés nominal (anual) Circular 8/90 7 de septiembre de 1.990
RENTAS:
– Renta temporal: número finito y conocido de capitales.
– Renta perpetura: número infinito o demasiado grande de capitales
– Un capital es pospagable si su vencimiento se produce al final del periodo.
– Un capital es prepagable si su vencimiento se produce al inicio del periodo.
– Una renta es cierta cuando la cuantía de los términos y sus vencimientos son conocidos.
– El momento de constitución (origen) de una renta no tiene porqué ser siempre el momento inicial (t=cero).
– Una renta geométrica perpetua sólo se puede calcular si 1+i > q
– Renta inmediata: si el origen coincide con el momento de valoración. Ej. Origen en t=0 y me piden t=0
– Renta anticipada: el origen es anterior al momento de valoración. Hay que capitalizarla. Ej. origen en t=0 y me piden t=2.
– Renta diferida: el origen es posterior al momento de valoración. Hay que actualizarla. Ej. origen en t=2 y me piden t=0
– Método prospectivo: trabajo con terminos futuros para calcular el valor de la renta ej. Vo
– Método retrospectivo: trabajo con terminos pasados para calcular el valor de la renta ej Vn
– Los términos son capitales financieros que no son equivalentes ya que no acumulan intereses.
– El valor actual de una renta con términos inmediatos y pospagables es menor que el obtenido cuando se consideran los mismos términos inmediatos pero prepagables.
PRÉSTAMOS:
– El importe recibido o entregado que inicia la operación se denomina principal o nominal o prestación.
– El importe concedido de un préstamo, para el banco es un activo financiero (derecho de cobro) y para el cliente un pasivo financiero (obligación de pago).
– Prestamista o acreedor: quien entrega la prestación
– Prestatario o deudor: quien recibe la préstación.
– Un sistema francés tiene la cuota de pago (Cp) constante.
– Un sistema italiano tiene la cuota de amortización (Ap) constante.
– Un sistema americano tiene cuota de interés (Ip) constante.
– En un préstamo que se amortiza por el sistema de cuotas de amortización constantes (sistema uniforme), los pagos o términos amortizativos siguen una progresión aritmética decreciente.
– Diferencia entre póliza y préstamo: en la póliza dispones del capital a demanda y en el préstamo dispones de todo el capital al inicio
– Diferencial siempre es constante durante la vida del préstamo pero el índice de referencia puede cambiar.
– Euribor: tipo de interés del mercado interbancario
– Sistema alemán es prepagable
– En sistema italiano cp decrece aritméticamente a una razón d= -iA
– En carencia parcial Dp es cte (hipótesis i =cte)
– En carencia total Dp es creciente de forma geométrica por la acumulación de los intereses (hipótesis i=cte)
– Un préstamo con carencia es una renta diferida.
¿Necesitas que te ayudemos?
Contrata un BONO INDIVIDUAL y prepara tus asignaturas con nosotros.